Pengertian Eksponen
Eksponen (atau perpangkatan) adalah operasi matematika yang melibatkan bilangan pokok dan pangkat. Secara umum, bilangan berpangkat dapat dinyatakan sebagai:
$$ a^n = a \times a \times a \times \cdots \times a \ (n \ \text{kali}) $$
Di mana:
- (a) adalah bilangan pokok (basis),
- (n) adalah pangkat (eksponen).
Sifat-sifat Eksponen
Beberapa sifat penting dari eksponen yang sering digunakan adalah:
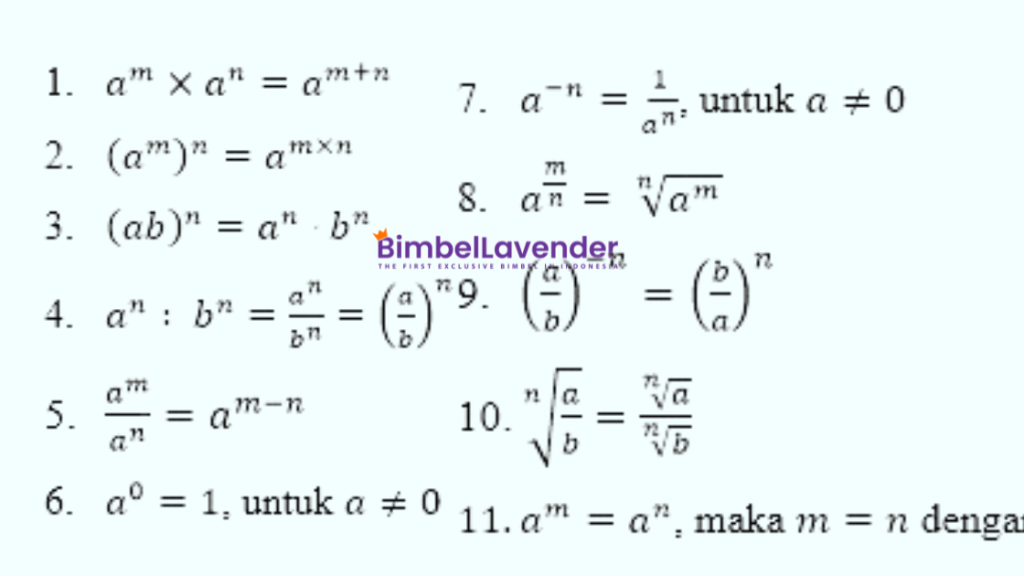
Contoh Soal Eksponen dan Pembahasan
Soal 1 (Mudah):
Sederhanakan ekspresi eksponen
$$ ( 3^2 \times 3^3 ) $$
Pembahasan:
$$ 3^2 \times 3^3 = 3^{2+3} = 3^5 = 243 $$
Soal 2 (Mudah):
Sederhanakan ekspresi
$$ ( \frac{5^6}{5^2} ) $$
Pembahasan:
$$ \frac{5^6}{5^2} = 5^{6-2} = 5^4 = 625 $$
Soal 3 (Mudah):
Sederhanakan ekspresi $$ (2^3)^2 $$
Pembahasan:
$$ (2^3)^2 = 2^{3 \times 2} = 2^6 = 64 $$
Soal 4 :
Sederhanakan ekspresi
$$ \left(\frac{4}{3}\right)^2 \times \left(\frac{4}{3}\right)^3 $$
Pembahasan:
$$ \left(\frac{4}{3}\right)^2 \times \left(\frac{4}{3}\right)^3 = \left(\frac{4}{3}\right)^{2+3} = \left(\frac{4}{3}\right)^5 $$
$$ \left(\frac{4}{3}\right)^5 = \frac{4^5}{3^5} = \frac{1024}{243} $$
Soal 5 (Sedang):
Hitung hasil dari
$$ 2^{-3} $$
Pembahasan:
$$ 2^{-3} = \frac{1}{2^3} = \frac{1}{8} $$
Soal 6:
Sederhanakan ekspresi
$$ 9^{\frac{3}{2}} $$
Pembahasan:
$$ 9^{\frac{3}{2}} = \left(\sqrt{9}\right)^3 = 3^3 = 27 $$
Soal 7 (Sedang):
Sederhanakan ekspresi
$$ \left(\frac{16}{25}\right)^{\frac{3}{2}} $$
Pembahasan:
$$ \left(\frac{16}{25}\right)^{\frac{3}{2}} = \left(\frac{\sqrt{16}}{\sqrt{25}}\right)^3 = \left(\frac{4}{5}\right)^3 = \frac{64}{125}
$$
Soal 8 (Sulit):
Jika $$ x = 2^3 \times 5^{-2} $$ , hitung nilai $$ x^{-1} $$
Pembahasan:
$$ x = 2^3 \times 5^{-2} = 8 \times \frac{1}{25} = \frac{8}{25} $$
$$ x^{-1} = \frac{1}{\frac{8}{25}} = \frac{25}{8} $$
Soal 9 (Sulit):
Sederhanakan $$ (27 \times 8)^{\frac{2}{3}} $$
Pembahasan:
$$ (27 \times 8)^{\frac{2}{3}} = 27^{\frac{2}{3}} \times 8^{\frac{2}{3}} = (3^3)^{\frac{2}{3}} \times (2^3)^{\frac{2}{3}} $$
$$ = 3^2 \times 2^2 = 9 \times 4 = 36 $$
Soal 10 (Standar UTBK):
Diketahui $$ ( a = 2^{x-2} ) $$ dan $$ ( b = 2^{x+3} ) $$ . Tentukan nilai $$ ( \frac{b}{a} ) $$
Pembahasan:
$$ \frac{b}{a} = \frac{2^{x+3}}{2^{x-2}} = 2^{(x+3)-(x-2)} = 2^{5} = 32 $$
Itulah materi dan contoh soal mengenai eksponen, mulai dari yang mudah hingga soal yang lebih sulit. Soal-soal ini membantu dalam memahami berbagai sifat eksponen dan penerapannya dalam berbagai bentuk soal.
