Materi TKA Matematika : Bilangan

Matematika selalu berawal dari pemahaman dasar mengenai bilangan dan cara mengoperasikannya. Dalam ujian TKA Matematika Wajib, salah satu materi penting yang sering menjadi dasar dari soal-soal lanjutan adalah jenis dan sifat bilangan, operasi bilangan, serta penerapan sifat komutatif, asosiatif, dan distributif. Meskipun tampak sederhana, konsep ini merupakan pondasi untuk menyelesaikan berbagai persoalan aritmetika hingga aljabar. Oleh karena itu, memahami materi ini secara menyeluruh akan sangat membantu dalam menjawab soal dengan lebih cepat dan tepat.

1. Jenis & Sifat Bilangan; Operasi Bilangan; Sifat Komutatif, Asosiatif, Distributif

Materi ini tidak dibahas secara khusus dalam bagian terpisah di buku ini, tetapi digunakan sebagai dasar dalam pembahasan eksponen, akar, dan aljabar. Berikut adalah penjelasan umum yang sesuai dengan kurikulum SMA:

Jenis Bilangan:

• Bilangan Bulat: …, -3, -2, -1, 0, 1, 2, 3, …
• Bilangan Rasional: Bilangan yang dapat dinyatakan sebagai pecahan abba​, dengan a,b∈Z,b≠0a,b∈Z,b=0
• Bilangan Irrasional: Bilangan yang tidak dapat dinyatakan sebagai pecahan, misalnya 

Sifat Operasi Bilangan:

1. Komutatif:
   • Penjumlahan: a+b=b+a
   • Perkalian: a×b=b×a
2. Asosiatif:
   • Penjumlahan: (a+b)+c=a+(b+c)
   • Perkalian: (a×b)×c=a×(b×c)
3. Distributif:
   • Perkalian terhadap penjumlahan: a×(b+c)=a×b+a×c
4. Aturan Operasi Hitung Campuran Dilangan Bulat
   • Operasi perkalian dan pembagian dikerjakan terlebih dahulu daripada operasi penjumlahan dan pengurangan.
   • Operasi perkalian dan pembagian pengerjaannya dimulai dari yang sebelah kiri.
   • Operasi penjumlahan dan pengurangan pengerjaannya dimulai dari yang sebelah kiri.

2. Pangkat & Akar

A. Pangkat (Eksponen)

Bentuk Umum:an=a×a×a×⋯×a(sebanyak n kali)an=a×a×a×⋯×a(sebanyak n kali)

• a: bilangan pokok
• n: pangkat

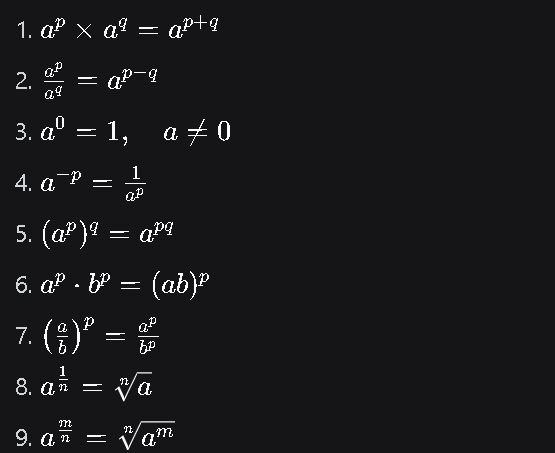
B. Bentuk Akar

Bentuk akar adalah akar dari bilangan rasional yang hasilnya irrasional.

Sifat-Sifat Bentuk Akar:

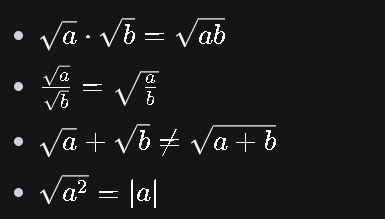
Merasionalkan Bentuk Akar:

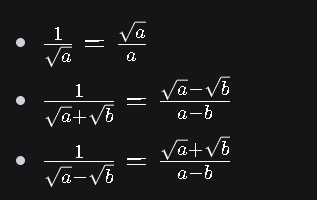
C. PECAHAN

a. Jenis-jenis Bilangan Pecaban

1. Pecahan biasa
2. Pecahan campuran bilangan bulat.
3. Pecahan campuran berasal dari pecahan biasa, yang mana nilai pembilang lebih besar daripada penyebutnya.
4. Pecahan desimal (0,25; 0,375; 0,4; dsb).
5. Persen (%) yaitu pecahan per seratus (25%, 10%, 90%, dsb).
6. Permil (%o) yaitu pecahan per seribu (25%0, 40%o, 15%o, dsb).

B.Pecahan Senilai

1. Pecahan senilai adalah pecahan yang mempunyai nilai yang sama.
2. Pecahan tidak akan berubah nilainya jika pembilang dan penyebut

Contoh soal dan Pembahasan

Nomor 1

Nomor 2

Nomor 3

Nomor 4

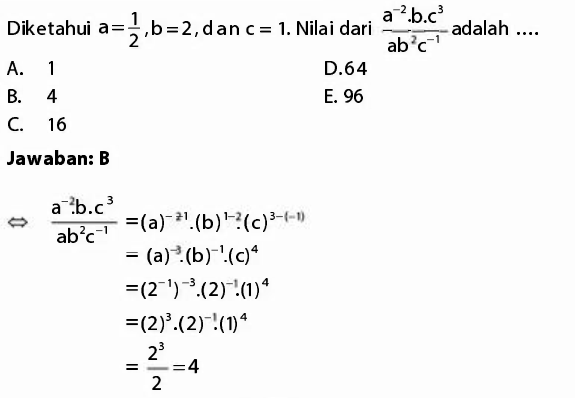
Dengan memahami jenis dan sifat bilangan, cara melakukan operasi bilangan, serta penerapan sifat komutatif, asosiatif, dan distributif, kita dapat membangun dasar yang kuat dalam menyelesaikan soal-soal matematika. Materi ini tidak hanya berguna untuk menghadapi ujian TKA Matematika Wajib, tetapi juga menjadi kunci dalam memahami konsep matematika yang lebih kompleks di jenjang berikutnya. Semakin terlatih kita menggunakan sifat-sifat dasar ini, semakin mudah pula kita menemukan solusi yang cepat, tepat, dan efisien dalam berbagai permasalahan.

Kak Sa’ad

Arif Saadilah adalah seorang alumnus Universitas Indonesia (UI) yang telah menyelesaikan gelar Sarjana (S1) dalam bidang Fisika dan gelar Magister (S2) dalam bidang Teknik Metalurgi Material di UI. Sejak tahun 2011, Arif Saadilah telah berperan sebagai pengajar di berbagai bimbingan belajar di seantero Depok, utamanya bimbingan masuk PTN. Namun sejak 2016 – 2020 memutuskan bergabung menjadi pembimbing kelas (pendamping sekaligus pengajar di kelas Amazing Camp) Bimbingan Belajar Lavender (Bimbel Lavender) dalam mata pelajaran Fisika, Materi SNBT (Pengetahuan Kuantitatif dan Penalaran Matematika), dan Matematika Dasar.