Ujian TKA untuk mata pelajaran Matematika bagi siswa SMA merupakan momen penting dalam mengevaluasi pemahaman konsep-konsep matematika secara menyeluruh. Melalui artikel ini, kami menghadirkan pembahasan mendalam beserta jawaban lengkap dari soal-soal TKA Matematika resmi dari kemendikdasmen, agar Anda dapat menelaah setiap langkah pengerjaan, memahami strategi penyelesaian, dan memperkuat kesiapan menghadapi tes sesungguhnya.
Contoh Soal TKA Resmi
Nomor 1
Soal TKA Nomor 2
Mirna akan memproduksi dua jenis kue dengan modal Rp8.000.000,00. Biaya produksi kue bolu sebesar Rp15.000,00 per kotak dan dijual dengan laba 40%. Sedangkan biaya produksi kue brownies sebesar Rp20.000,00 per kotak dan dijual dengan laba 35%. Setiap harinya, Mirna dapat memproduksi paling banyak 500 kotak kue.
Apabila Mirna ingin memperoleh keuntungan maksimum, tentukan
Benar atau Salah untuk setiap pernyataan berikut!
| # | Pernyataan | Benar | Salah |
| A. | Mirna harus memproduksi 200 kotak kue bolu. | ||
| B. | Mirna harus memproduksi kue brownies lebih banyak. | ||
| C. | Keuntungan maksimum yang dapat diperoleh Mirna adalah Rp3.100.000,00. |
Soal TKA Nomor 3
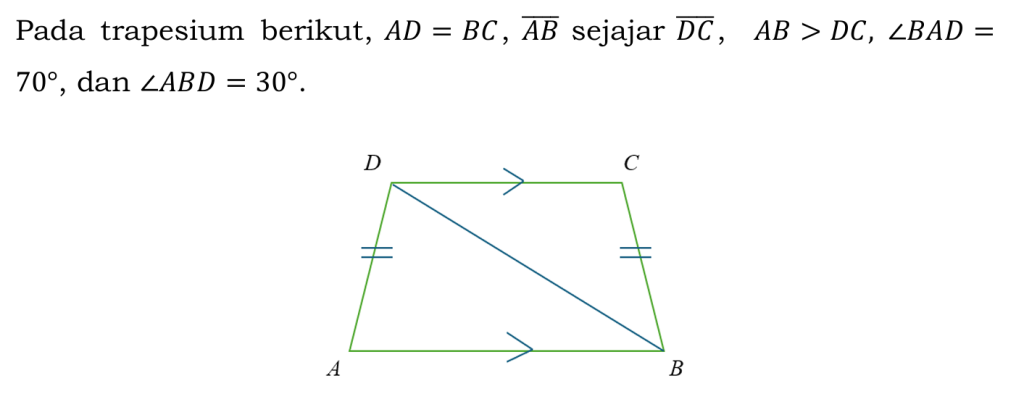
Tentukan Benar atau Salah untuk setiap pernyataan berikut terkait dengan besar sudut pada trapesium 𝐴𝐵𝐶𝐷!
| # | Pernyataan | Benar | Salah |
| A. | |||
| B. | |||
| C. |
Nomor 4
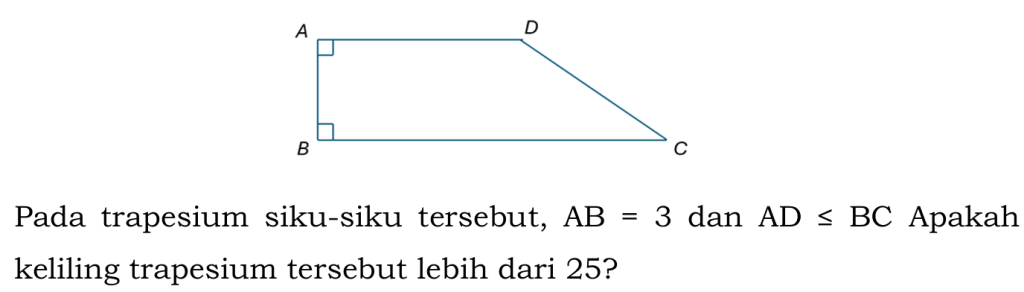
Putuskan apakah dengan tambahan informasi Pernyataan (1) dan
Pernyataan (2) berikut cukup untuk menjawab pertanyaan tersebut!
(1) Luas trapesium ABCD = 24.
(2) BC = 10 dan CD = 5.
A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi Pernyataan (2) SAJA tidak cukup.
B. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi Pernyataan (1) SAJA tidak cukup.
C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan Pernyataan (2) SAJA cukup.
E. Pernyataan (1) dan Pernyataan (2) tidak cukup untuk menjawab pertanyaan.
Nomor 5
Suatu tangga dengan panjang 6 meter disandarkan pada dinding vertikal. Sudut yang dibentuk tangga dengan lantai adalah 60°.

Tinggi dinding yang disentuh ujung atas tangga adalah ….
A. 3 meter
B. 3√2 meter
C. 3√3 meter
D. 4√2 meter
E. 4√3 meter
Nomor 6
Rata-rata nilai ulangan 17 murid dari skala 100 adalah 83. Ada 3 murid yang mengikuti ujian susulan sehingga rata-rata nilai ulangan dari 20 murid menjadi 82. Tentukan semua pernyataan berikut yang benar terkait dengan nilai ketiga murid yang mengikuti ujian susulan! Jawaban benar lebih dari satu.
- Jumlah nilai ketiga murid yang mengikuti ujian susulan adalah 229.
- Rata-rata nilai ketiga murid yang mengikuti ujian susulan lebih dari 70.
- Nilai terendah dari ketiga murid yang mengikuti ujian susulan tidak kurang dari 29.
- Nilai tertinggi dari ketiga murid yang mengikuti ujian susulan lebih dari 76.
- Jangkauan data nilai ketiga murid yang mengikuti ujian susulan lebih dari dari 72.
Nomor 7
Tentukan Benar atau Salah pada setiap pernyataan berikut yang terkait dengan grafik fungsi !
Tentukan Benar atau Salah pada setiap pernyataan berikut yang terkait dengan grafik fungsi !
| # | Pernyataan | Benar | Salah |
| A. | Grafik fungsi ƒ terbuka ke atas. | ||
| B. | Grafik fungsi ƒ memotong garis y = -18 | ||
| C. | Grafik fungsi ƒ tidak melalui kuadran tiga. |
Nomor 8
Tagihan listrik bulanan di sebuah apartemen dihitung berdasarkan jumlah energi listrik (dalam kWh) yang digunakan. Apartemen tersebut masih menggunakan meteran listrik yang berbeda dari penggunaan token.Biaya tagihan listrik dihitung dengan rumus:
Keterangan:
F(x) = total tagihan dalam Rupiah
x = Jumlah pemakaian energi listrik (KWh)Andi merupakan salah satu penghuni apartemen tersebut yang menerima tagihan pembayaran listrik seperti terlihat pada gambar berikut:

Dia menyadari bahwa penggunaan listrik sebulan terakhir lebih dari penggunaan listrik biasanya.
Berdasarkan informasi tersebut, biasanya berapa besar penggunaan listrik di apartemen Andi?
Pilihlah jawaban yang benar! Jawaban benar lebih dari satu.
- 85 kWh
- 90 kWh
- 100 kWh
- 120 kWh
- 137 kWh
Nomor 9
Pak Andi akan mempresentasikan desain gedung berukuran 60 cm × 60 cm menggunakan proyektor ke layar berukuran 2,4 meter × 1,8 meter yang dipasang di depan ruang rapat (orientasi horizontal). Proyektor menghasilkan pembesaran proporsional tergantung jaraknya dari layar.
Pak Andi menempatkan proyektor dengan jarak yang menghasilkan skala pembesaran seperti terlihat pada gambar berikut:

Bagaimanakah tampilan desain gedung di layar?
Tentukan Benar atau Salah pada setiap pernyataan berikut!
| # | Pernyataan | Benar | Salah |
| A. | Perbandingan ukuran tampilan desain di layar adalah 1 : 1. | ||
| B. | Ukuran panjang dan lebar tampilan desain pada layar adalah lebih dari 1 meter. | ||
| C. | Terdapat bagian gambar asli desain yang terpotong dalam tampilan pada layar. |
Nomor 10
Luki adalah panitia bazar di sekolahnya. Dia mendapat tugas dari ketua pelaksana untuk membuat kupon. Dia ingin di setiap kupon memiliki kode akses yang unik. Kode akses kupon bazar itu memiliki lima karakter dengan format sebagai berikut:

dengan A, B, dan C menyatakan huruf, serta X dan Y menyatakan angka. Tidak boleh ada angka dan huruf yang diulang. Berapakah berapa banyak kode akses berbeda yang dapat dibuat?
A. 1.263.600
B. 1.352.000
C.1.404.000
D. 1.423.656
E. 1.757.600
Pembahasan
Nomor 1

Pembahasan Soal TKA Nomor 2
Inti soal ini adalah masalah optimisasi (linier) dengan variabel:
- xxx = jumlah kotak kue bolu
- yyy = jumlah kotak kue brownies
Diketahui:
- Modal (batas biaya) == = Rp 8.000.0008.000.0008.000.000.
- Biaya produksi bolu == = Rp 15.000/ kotak.
- Biaya produksi brownies == = Rp 20.000/ kotak.
- Laba bolu = 40% dari biaya → laba per bolu =0,4×15.000=6.000=0{,}4\times15.000=6.000=0,4×15.000=6.000.
- Laba brownies = 35% dari biaya → laba per brownies =0,35×20.000= 7000
- Kapasitas produksi per hari: paling banyak 500 kotak → x+y≤500

Kesimpulan terhadap pernyataan
A. “Mirna harus memproduksi 200 kotak kue bolu.” — Salah.
Solusi optimal menunjukkan Mirna harus memproduksi 400 kotak bolu.
B. “Mirna harus memproduksi kue brownies lebih banyak.” — Salah.
Pada solusi optimal Mirna justru memproduksi 400 bolu dan 100 brownies, jadi bolu lebih banyak.
C. “Keuntungan maksimum yang dapat diperoleh Mirna adalah Rp3.100.000,00.” — Benar.
Perhitungan menunjukkan keuntungan maksimum = Rp 3.100.000 pada (x,y)=(400,100)
Nomor 3

Pembahasan Nomor 4

Pembahasan Nomor 5

Pembahasan Nomor 6
Kita hitung dulu total dan rata-rata untuk menemukan informasi dasar.
- Jumlah nilai 17 murid dengan rata-rata 83 adalah
17×83=1411
(Perhitungan: 17×80=1360, ditambah 17×3=51, total 1360+51=1411.) - Setelah ditambah 3 murid rata-rata menjadi 82 untuk 20 murid, maka total semua nilai =
20×82=164020 - Jadi jumlah nilai ketiga murid susulan = 1640−1411=229
Sekarang tinjau pernyataan satu per satu.
1. Jumlah nilai ketiga murid yang mengikuti ujian susulan adalah 229. — Benar.
Langsung dari pengurangan total (diturunkan di atas): 1640−1411=229
2. Rata-rata nilai ketiga murid yang mengikuti ujian susulan lebih dari 70. — Benar.
Rata-rata ketiganya =229/3. Hitung:
229÷3=76,33.. sehingga jelas lebih dari 70.
3. Nilai terendah dari ketiga murid susulan tidak kurang dari 29. — Benar.
Buktinya dengan batas atas nilai siswa (maksimal 100). Jika salah satu murid mempunyai nilai <29, misal ≤28 \l, maka jumlah dua murid lainnya paling tinggi 100+100=200. Maka jumlah ketiganya paling besar 200+28=228, tetapi kita butuh jumlah 229. Karena 228<229 maka mustahil ada nilai salah satu murid ≤28. Jadi nilai terendah minimal 29, atau ditulis: nilai terendah tidak kurang dari 29.
(Contoh konkret yang memenuhi sum=229 dan mencapai batas ini: 29,100,100.)
4. Nilai tertinggi dari ketiga murid susulan lebih dari 76. — Benar.
Jika semua tiga murid ≤ 76, maka jumlah maksimal mereka 3×76=228, tapi kita butuh jumlah 229. Karena 228<229, tidak mungkin semua ≤76. Jadi setidaknya satu nilai harus >76.
5. Jangkauan data (range) nilai ketiga murid susulan lebih dari 72. — Salah.
Tidak ada keharusan range >72. Sebagai kontra-contoh (sesuai kondisi sum=229) ambil nilai 29,100,100. Jumlahnya 29+100+100=229. Range = 100−29=71, yaitu kurang dari 72. Jadi pernyataan “range > 72” tidak selalu benar.
Pembahasan Soal TKA Nomor 7

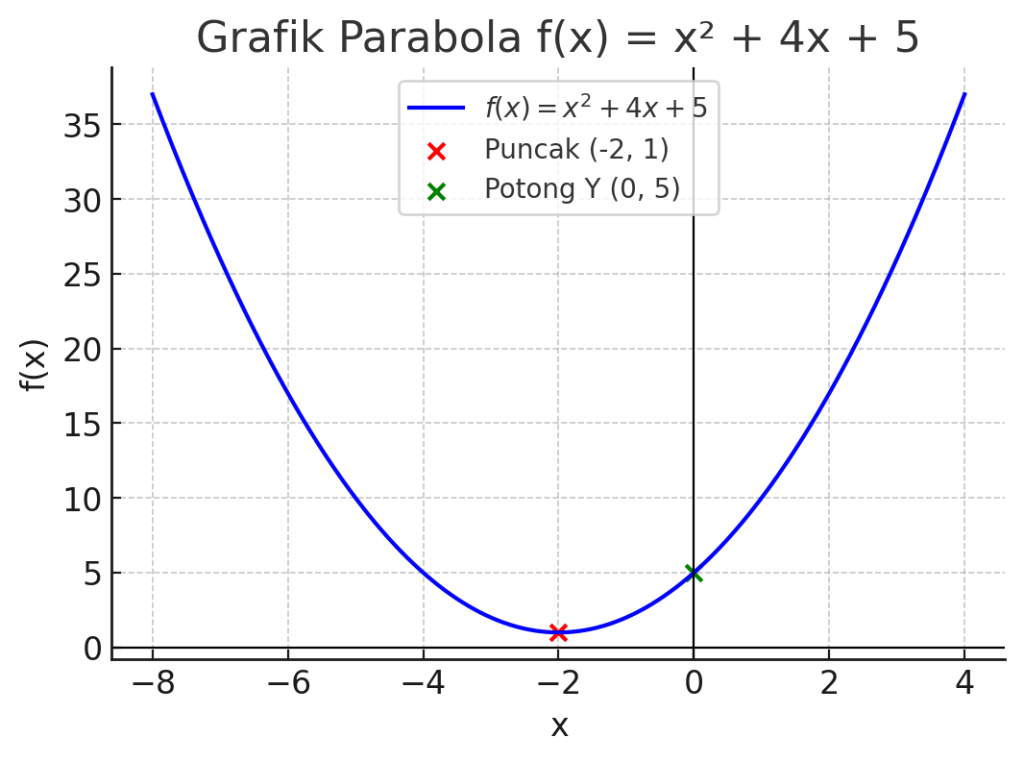
A. Grafik fungsi ƒ terbuka ke atas → Benar
Grafik berbentuk parabola dengan mulut menghadap ke atas (U terbuka ke atas). Itu artinya koefisien x^2 positif. Jadi pernyataan ini benar.
B. Grafik fungsi ƒ memotong garis y=−18 → Salah
“Memotong garis y=−18” artinya ada titik di grafik yang punya ordinat (nilai yyy) sama dengan −18. Kalau dilihat dari grafik, nilai y minimum (titik puncak parabola) lebih tinggi dari −18. Jadi grafik tidak pernah mencapai garis y=−18. Itu sebabnya pernyataan ini salah.
C. Grafik fungsi ƒ tidak melalui kuadran tiga → Benar
Kuadran III adalah daerah x<0,y<0. Dari gambar, bagian grafik di x<0 (sebelah kiri sumbu y) tetap berada di atas sumbu x (artinya y bernilai positif). Jadi grafik tidak pernah masuk ke kuadran III. Maka pernyataan ini benar.
🔑 Jadi alasannya:
- (A) Benar karena parabola terbuka ke atas.
- (B) Salah karena grafik tidak pernah mencapai y=−18y=-18y=−18.
- (C) Benar karena grafik tidak menyentuh kuadran III.
Pembahasan Soal TKA Nomor 8

Nomor 9
Diketahui:
- Ukuran gambar asli: 60 cm×60 cm=0,6 m×0,6 m.
- Jarak proyektor ke layar = 3 m.
- Skala pembesaran = 0,6×jarak
Skala=0,6×3=1,8
1. Hitung ukuran hasil proyeksi:
Jadi, proyeksi gambar di layar = 1,08 m×1,08 m.
2. Bandingkan dengan layar (2,4 m × 1,8 m):
- Layar lebih lebar dan tinggi daripada hasil proyeksi.
- Artinya, gambar tidak terpotong, justru masih ada ruang kosong di layar.
3. Evaluasi pernyataan:
A. Perbandingan ukuran tampilan desain di layar adalah 1 : 1.
✅ Benar. Karena gambar asli berbentuk persegi (1 : 1), hasil proyeksi tetap berbentuk persegi dengan rasio 1 : 1.
B. Ukuran panjang dan lebar tampilan desain pada layar adalah lebih dari 1 meter.
✅ Benar. Hasil proyeksi = 1,08 m × 1,08 m (> 1 m).
C. Terdapat bagian gambar asli desain yang terpotong dalam tampilan pada layar.
❌ Salah. Karena ukuran layar (2,4 × 1,8) lebih besar dari hasil proyeksi (1,08 × 1,08), tidak ada bagian yang terpotong.
👉 Jadi jawabannya:
- A = Benar
- B = Benar
- C = Salah ✅
Nomor 10
Format kode: A X B Y C
- A,B,CA, B, CA,B,C = huruf (tanpa pengulangan)
- X,YX, YX,Y = angka (tanpa pengulangan)
- Tidak boleh ada huruf dan angka yang diulang.
1. Pilihan huruf (A, B, C)
Jumlah huruf alfabet = 26.
Kita pilih 3 huruf berbeda → urutan berarti (karena A-B-C berbeda posisi). 26×25×24=15600
2. Pilihan angka (X, Y)
Jumlah angka = 10 (0–9).
Kita pilih 2 angka berbeda → urutan berarti. 10×9=90
3. Total kemungkinan kode
15600×90=1.404.000
✅ Jadi jumlah kode akses berbeda yang dapat dibuat adalah 1.404.000.
Itu sebabnya jawaban yang benar adalah 1.404.000.
Kak Sa’ad
Arif Saadilah adalah seorang alumnus Universitas Indonesia (UI) yang telah menyelesaikan gelar Sarjana (S1) dalam bidang Fisika dan gelar Magister (S2) dalam bidang Teknik Metalurgi Material di UI. Sejak tahun 2011, Arif Saadilah telah berperan sebagai pengajar di berbagai bimbingan belajar di seantero Depok, utamanya bimbingan masuk PTN. Namun sejak 2016 – 2020 memutuskan bergabung menjadi pembimbing kelas (pendamping sekaligus pengajar di kelas Amazing Camp) Bimbingan Belajar Lavender (Bimbel Lavender) dalam mata pelajaran Fisika, Materi SNBT (Pengetahuan Kuantitatif dan Penalaran Matematika), dan Matematika Dasar.





